Mathematical Physics
At a glace
Study Programme
| Target degree: | Master of Science (M.Sc.) |
| Standard lenghts of programme: | 4 Semester |
| Teaching language: | German |
| Start of study: | for the summer and winter semester |
Admission/Application
| Restricted Admission: | non, demonstration of proficiency in the relevant field required | ||||
| Aptitude Assessment: | see website Student Affairs |
Programme Content
In contrast to other mathematics degree programmes, the consecutive Bachelor's/Master's degree programme in Mathematical Physics focuses primarily on the interplay between the two key sciences of mathematics and physics. The two are inextricably linked: Mathematics is the universal language of physics and provides efficient methods for dealing with physical and technical issues. Physics, in turn, is one of the most important driving forces behind the development of new mathematical theories and is one of the main areas of application for mathematics.
The "Master of Science" programme prepares students for scientific activities in the field of mathematical physics and the "Master of Science" degree prepares students for a doctorate (Dr. rer. nat.).
Learning Objectives
The aim of the programme is to provide students with in-depth knowledge and insight into the internal interrelationships of various sub-areas of mathematics, physics and mathematical physics as well as insight into interdisciplinary relationships, the mathematical and theoretical foundations of mathematical physics and interdisciplinary contexts as well as a sound knowledge of the mathematical, theoretical and experimental methods for gaining new insights including the necessary capacity for abstraction, analytical thinking, a high level of problem-solving competence and the ability to structure complex interrelationships, so that they can work as responsible mathematical physicists in interdisciplinary and international teams of (natural) scientists in research, industry and the economy.
| Module Groups | Abbreviation | ECTS-Points |
|---|---|---|
| Mandatory Courses | 20 | |
| Analysis and Geometry of Classical Systems | 10-M=MP1 | 10 |
| Algebra and Dynamics of Quantum Systems | 10-M=MP2 | 10 |
| Module Groups | Abbreviation | ECTS-Points |
|---|---|---|
| Electives Field | 50 | |
| Mathematics | mind. 8 | |
| Applied Analysis | 10-M=AAAN | 10 |
| Topics in Algebra | 10-M=AALG | 10 |
| Differential Geometry | 10-M=ADGM | 10 |
| Complex Analysis | 10-M=AFTH | 10 |
| Geometric Structures | 10-M=AGMS | 10 |
| Industrial Statistics 1 | 10-M=AIST | 10 |
| Lie Theory | 10-M=ALTH | 10 |
| Numeric of Large Systems of Equations | 10-M=ANGG | 10 |
| Basics in Optimization | 10-M=AOPT | 10 |
| Control Theory | 10-M=ARTH | 10 |
| Stochastic Models of Risk Management | 10-M=ASMR | 10 |
| Stochastical Processes | 10-M=ASTP | 10 |
| Topology | 10-M=ATOP | 10 |
| Time Series Analysis | 10-M=AZRA | 10 |
| Number Theory | 10-M=AZTH | 10 |
| Giovanni Prodi Lecture (Master) | 10-M=AGPCin | 5 |
| Algebraic Topology | 10-M=VATP | 10 |
| Geometrical Mechanics | 10-M=VGEM | 10 |
| Industrial Statistics 2 | 10-M=VIST | 10 |
| Field Arithmetics | 10-M=VKAR | 10 |
| Numeric of Partial Differential Equations | 10-M=VNPE | 10 |
| Mathematical Statistics | 10-M=VSTA | 10 |
| Discrete Mathematics | 10-M=VDIM | 5 |
| For further modules, please refer to the relevant degree Subject Description (SFB) | ||
| Physics | mind. 8 | |
| General Theoretical Physics | ||
| Quantum Mechanics II | 11-QM2 | 8 |
| Theoretical Quantum Optics | 11-TQO | 8 |
| Theory of Relativity | 11-RTT | 6 |
| Renormalization Group Methods in Field Theory | 11-RMFT | 8 |
| Physics of Complex Systems | 11-PKS | 6 |
| Advanced Theory of Quantum Computing and Quantum Information | 11-QIC | 6 |
| Theoretical Solid State Physics | ||
| Theoretical Solid State Physics | 11-TFK | 8 |
| Theoretical Solid State Physics 2 | 11-TFK2 | 8 |
| Phenomenology and Theory of Superconductivity | 11-PTS | 6 |
| Topological Effects in Solid State Physics | 11-TEFK | 8 |
| Field Theory in Solid State Physics | 11-FFK | 8 |
| Computational Materials Science (DFT) | 11-CMS | 8 |
| Conformal Field Theory | 11-KFT | 6 |
| Conformal Field Theory 2 | 11-KFT2 | 6 |
| Particle Physics (Standard Model) | 11-TPSM | 8 |
| Renormalization Group and Critical Phenomena | 11-CRP | 6 |
| Bosonisation and Interactions in One Dimension | 11-BWW | 6 |
| Introduction to Gauge/Gravity Duality | 11-GGD | 8 |
| Astrophysics | ||
| Cosmology | 11-AKM | 6 |
| Theoretical Astrophysics | 11-AST | 6 |
| Introduction to Plasma Physics | 11-EPP | 6 |
| High Energy Astrophysics | 11-APL | 6 |
| Computational Astrophysics | 11-NMA | 6 |
| Theoretical Elementary Particle Physics | ||
| Quantum Field Theory I | 11-QFT1 | 8 |
| Quantum Field Theory II | 11-QFT2 | 8 |
| Theoretical Elementary Particle Physics | 11-TEP | 8 |
| String Theory 1 | 11-STRG1 | 8 |
| String Theory 2 | 11-STRG2 | 6 |
| Models Beyond the Standard Model of Elementary Particle Physics | 11-BSM | 6 |
| For further modules, please refer to the relevant degree Subject Description (SFB) | ||
| Research in Groups | mind. 10 | |
| Research in Groups - Algebra | 10-M=GALG | 10 |
| Research in Groups - Discrete Mathematics | 10-M=GDIM | 10 |
| Research in Groups - Dynamical Systems and Control Theory | 10-M=GDSC | 10 |
| Research in Groups - Complex Analysis | 10-M=GCOA | 10 |
| Research in Groups - Geometry and Topology | 10-M=GGMT | 10 |
| Research in Groups - Mathematics in Context | 10-M=GMCX | 10 |
| Research in Groups - Mathematics in the Sciences | 10-M=GMSC | 10 |
| Research in Groups - Measure and Integral | 10-M=GMAI | 10 |
| Research in Groups - Numerical Mathematics and Applied Analysis | 10-M=GNMA | 10 |
| Research in Groups - Robotics, Optimization and Control Theory | 10-M=GROC | 10 |
| Research in Groups - Time Series Analysis | 10-M=GTSA | 10 |
| Research in Groups - Statistics | 10-M=GSTA | 10 |
| Research in Groups - Number Theory | 10-M=GNTH | 10 |
| For further modules, please refer to the relevant degree Subject Description (SFB) |
| Modules | Abbreviation | ECTS-Points |
|---|---|---|
| Professional Specialization Mathematical Physics | 11-FS-MP | 10 |
| Scientific Methods and Project Management Mathematical Physics | 11-MP-MP | 10 |
| Master Thesis Mathematical Physics | 11-MA-MP | 30 |
The final section consists of the modules "Professional Specialisation in Mathematical Physics" and "Scientific Methods and Project Management Mathematical Physics" as well as the Master's thesis. The final year lasts one year and is usually completed in the 3rd and 4th semesters. The Master's thesis must be completed in 6 months. The modules "Professional Specialization" and "Scientific Methods and Project Management" are aligned with the Master's thesis in terms of content and should be successfully completed before the start of the Master's thesis.
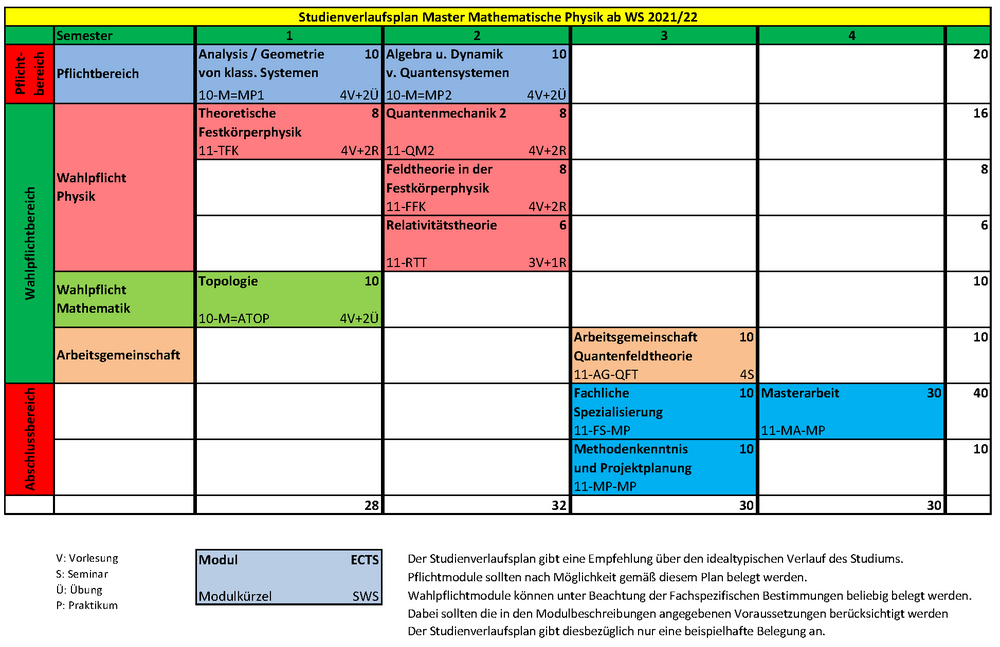
The course of study shown (Download als pdf) s a recommendation resulting from the logical sequence of module topics.
You are free to organise your studies according to your own wishes, bring certain modules forward or take them later, e.g. after a semester abroad.