Quantum Field Theory and String Theory
A long-standing open problem in theoretical physics is the consistent formulation of a quantum theory of gravitation in view of a unified theory of all fundamental interactions. String theory is a promising candidate for achieving this goal. String theory has also lead to the formulation of the AdS/CFT correspondence, which provides an important example of Gauge/Gravity Duality. A duality is a map between two physical theories (Lagrangians) which describe the same physical system and its dynamics, while formally involving different degrees of freedom. Gauge/gravity duality is the first example of a duality relating a quantum field theory in flat space to a gravity theory. This provides a new viewpoint on the formulation of quantum gravity. An essential ingredient of this very special duality is the holographic principle, which states that the information content of a volume is stored on its boundary. The holographic principle is famously realized by black holes for which - according to the celebrated Bekenstein-Hawking formula - the entropy is proportional to the area of their event horizon. Similarly, in gauge/gravity duality, the quantum field theory is defined on the d-dimensional boundary of a (d+1)-dimensional curved space.
A further important aspect of gauge/gravity duality is that in a certain limit, it matches strongly coupled quantum field theories, in which calculations are generically hard, to classical gravity theories that are much easier to solve. This has applications in many different areas of physics, in addition to particle physics also to condensed matter physics.
Our group performs research on many aspects of quantum field theory and gauge/gravity duality. We list a few of them here:
- Gauge/gravity duality and quantum information. As described above, information in relation to black holes plays and essential role within gauge/gravity duality. We work on establishing more precise maps between black hole information and quantum information theory. The aim is on one hand a better understanding of the quantum nature of black holes and of the emergence of space-time, and on the other the establishment of new useful observables and measures in quantum field theory and quantum information.
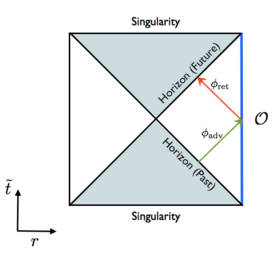
- Applications of gauge/gravity duality to QCD. Gauge/gravity duality has successfully be used to calculate retarded and advanced Green’s functions in finite-temperature field theory (see figure), in particular in view of describing the physics of the quark-gluon plasma, i.e. the state of strongly interacting matter at high temperatures. In particular, transport coefficients such as the fluid shear viscosity were calculated and successfully compared to experimental results. In a different development, our group has made important contributions to establishing the gravity dual of chiral symmetry breaking. This allows to calculate meson masses and decay constants and to provide comparisons with lattice gauge theory and even experiment. A current extension of this approach is to study properties of the Higgs particle by assuming that it is composite. Gauge/gravity duality together with string theory may provide a UV completion of the effective field theory models involved. This approach is currently used to calculate Higgs decay processes in view of comparison with lattice results and with experiment.
- Applications of gauge/gravity duality to condensed matter physics. The use of gauge/gravity duality for calculating transport coefficients for strongly correlated systems at finite temperature and density may also be applied in the context of condensed matter physics. A question currently under intense study is if and how electrons in a solid may be described as a fluid using hydrodynamics. Moreover, in relation to research on topological systems carried out in Würzburg, we investigate field-theory topological structures such as quantum anomalies and their implications for the conduction properties of materials.