Research
Summary of the work of our chair:
At our chair, we are establishing new cross-connections between quantum field theory on the one hand and gravitation on the other, so-called dualities. On the one hand, we are gaining new insights into the quantum nature of gravity. On the other hand, we are using the dualities to develop new methods for describing strongly coupled systems. These occur frequently in physics, but are often difficult to describe with established methods. Our methods find applications both in condensed matter physics and in elementary particle physics. Another research focus is new connections between quantum information and statistical mechanics.
News
Recent publications:
- Geometric Phases Characterise Operator Algebras and Missing Information
Souvik Banerjee, Moritz Dorband, Johanna Erdmenger, Anna-Lena Weigel
arXiv:2306.00055
- Geometric Quantum Discord Signals Non-Factorization
Souvik Banerjee, Pablo Basteiro, Rathindra Nath Das, Moritz Dorband
arXiv:2305.04952
- Symmetry-resolved modular correlation functions in free fermionic theories
Giuseppe Di Giulio, Johanna Erdmenger
arXiv:2305.02343
Information for students - black holes and quantum information
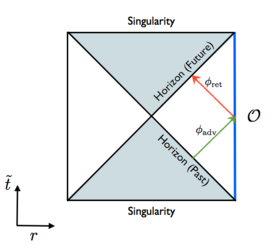
The AdS/CFT correspondence is one of the most revolutionary physical discoveries of the last 25 years. It is arguably the most promising approach to fathoming the quantum nature of gravity and is one of the foundations of our understanding of the connection between gravity and quantum mechanics. Since the AdS/CFT correspondence is based on the physics of black holes and quantum information, we will explain the related concepts using the black hole information paradox, one of the greatest mysteries of modern physics. Finally, we will see that parts of the paradox are solved by means of the AdS/CFT correspondence and exactly which questions the Chair of Theoretical Physics III at the University of Würzburg is researching.
Research software
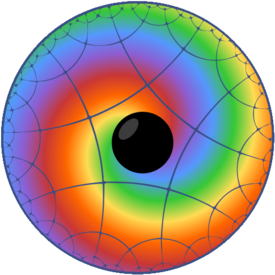
Our chair is the home of hypertiling - a high-performance Python 3 library for the generation and visualization of hyperbolic tilings embedded in the Poincaré disk model. Using efficient, precise and robust algorithms, isometric lattices with millions of polygons can be created in a matter of minutes on a single computer and are ready to be used for all sorts of scientific as well as artistic purposes.
Make sure you visit the website of the project: www.hypertiling.de and follow us on Twitter and YouTube for latest news, updates and animated videos.
