Research
Summary of the work of our chair:
At our chair, we are establishing new cross-connections between quantum field theory on the one hand and gravitation on the other, so-called dualities. On the one hand, we are gaining new insights into the quantum nature of gravity. On the other hand, we are using the dualities to develop new methods for describing strongly coupled systems. These occur frequently in physics, but are often difficult to describe with established methods. Our methods find applications both in condensed matter physics and in elementary particle physics. Another research focus is new connections between quantum information and statistical mechanics.
News
Recent publications:
- Wormhole-induced effective coupling in SYK chains
Pablo Basteiro, Giuseppe Di Giulio (Stockholm U.), Johanna Erdmenger, René Meyer, Zhuo-Yu Xian (FU Berlin)
arXiv:2410.23397
- Towards complexity of primary-deformed Virasoro circuits
Johanna Erdmenger, Jani Kastikainen, Tim Schuhmann (Ghent U.)
arXiv:2409.08319
- The chiral torsional anomaly and the Nieh-Yan invariant with and without boundaries
Johanna Erdmenger, Ioannis Matthaiakakis (Southampton U.), René Meyer, Dmitri Vassilevich (Universidade Federal do ABC, Santo André)
arXiv:2409.06766
- Krylov Complexity as a Probe for Chaos
Mohsen Alishahiha (IPM Teheran), Souvik Banerjee, Mohammad Javad Vasli (IPM Teheran)
arXiv:2408.10194
Information for students - black holes and quantum information
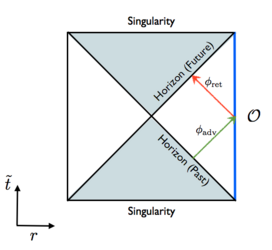
The AdS/CFT correspondence is one of the most revolutionary physical discoveries of the last 25 years. It is arguably the most promising approach to fathoming the quantum nature of gravity and is one of the foundations of our understanding of the connection between gravity and quantum mechanics. Since the AdS/CFT correspondence is based on the physics of black holes and quantum information, we will explain the related concepts using the black hole information paradox, one of the greatest mysteries of modern physics. Finally, we will see that parts of the paradox are solved by means of the AdS/CFT correspondence and exactly which questions the Chair of Theoretical Physics III at the University of Würzburg is researching.
Research software
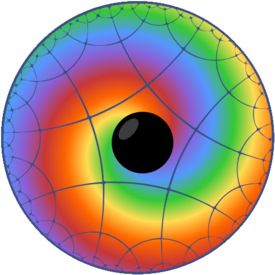
Our chair is the home of hypertiling - a high-performance Python 3 library for the generation and visualization of hyperbolic tilings embedded in the Poincaré disk model. Using efficient, precise and robust algorithms, isometric lattices with millions of polygons can be created in a matter of minutes on a single computer and are ready to be used for all sorts of scientific as well as artistic purposes.
Make sure you visit the website of the project: www.hypertiling.de and follow us on Twitter and YouTube for latest news, updates and animated videos.
