Research

Electron spectroscopy in the laboratory and at synchrotron radiation facilities, shedding light on...
- electronic structure of solid state systems, surfaces and thin films
- multi-particle-physics: Kondo-systems, heavy fermions, superconductors, quantum phase transitions
- strongly correlated electronic systems, topological insulators
- reactions on surfaces, interactions at interfaces, organic electronics, nanoanalytics
- basic research on condensed matter physics
Some examples of current research activities are given below.
Besides other surface characterizing techniques (LEED, STM, AFM, EELS, XAS, XMCD/XMLD, RIXS), the most important analytical method of the EP7 is photoemission spectroscopy (PES).
PES has a broad range of applications in chemistry and condensed matter physics, in particular in surface science and solid state physics. Depending on the used photon source, one gets e.g. information about the chemical composition of the sample (x-rays: XPS or ESCA, electron spectroscopy for chemical analysis) or the valence band structure of a single crystal (ultraviolet: UPS).
The group focuses on fundamental research using angle resolved experiments (ARPES) with high energy resolution.
An overview can be found in New J. Phys 7 (2005) 97.
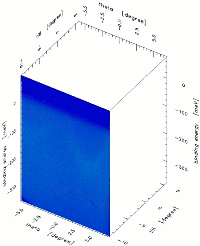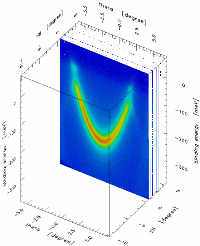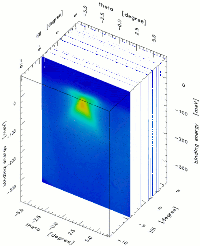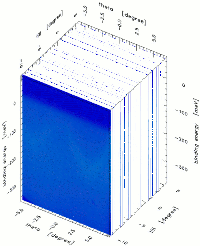
As a typical example, the image shows two data sets of the Fermi surfaces of CePt5 and LaPt5 acquired with ARPES. In the images, the bright colours (yellow and orange) and dark colours (black and dark red) correspond to the photoemission intensity at different positions of the Brillouin zone with higher or lower electron densities, respectively. This momentum-dependent information (so-called Fermi surface maps) allows directly the measurement of the dispersion (energy vs. momentum) and, therewith, the mapping of the Fermi surface topology.
The purpose of the experiments in the present case is to understand how the single 4f electron of Cerium induces so strong correlations to fundamentally change the macroscopic properties of Ce-compounds (e.g. the electrical resistivity) in terms of microscopic theories (quantum theory of matter). By comparing the experimental intensities of CePt5 to those of LaPt5, it is possible to learn what are the electron states responsible for the unusual properties of CePt5 and how they can be described by theoretical models (Kondo, SIAM), or whether more sophisticated theories are requested (Periodic Anderson Model PAM).
See projects in FOR1162 for more information
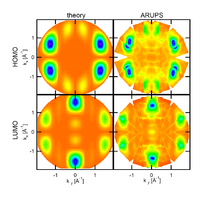
One capability of angular resolved photoelectron spectroscopy (ARPES) is analyzing the geometric structure of molecular orbitals. It has been shown, that the angular dependent intensity distribution of the photoemission signal can be understood as the Fourier transform of the molecular orbital. This allows, e.g., a straightforward comparison between the experimental results and quantum mechanic calculations.
As an example, the figure shows the 2D-plot of the theoretical and experimental ARPES intensities for the HOMO and LUMO of the organic prototyp molecule PTCDA. The experiment was performed for a highly ordered monolayer of molecules adsorbed on a Ag(110) single crystal surface. This intensity distribution gives a detailed insight into a change of the spacial distribution of the orbitals due to the interaction with the surface.
J. Ziroff et al., Hybridization of Organic Molecular Orbitals with Substrate States at Interfaces: PTCDA on Silver. Phys. Rev. Lett. 104, 2010.
M. Wießner et al., Electronic and geometric structure of the PTCDA/Ag(110) interface probed by angle-resolved photoemission. Physical Review B 86, 2012
Omicron: Result of the month.
With resonant inelastic x-ray scattering (RIXS) in the soft x-ray range, the chemical and electronic structure of solids, liquids, and gases can be investigated.
RIXS experiments generally need a high photon flux and thus have to be performed at a third generation synchrotron light source like the Advanced Light Source at LBNL in Berkeley.
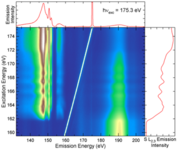
As an example, the figure on the right shows the RIXS “map” of CdS. The emission intensity is proportional to the color scale, and it is plotted as a function of emission energy (horizontal scale) and excitation energy (vertical scale). The upper panel shows a nonresonant x-ray emission spectrum at the excitation energy hv = 175.3 eV. The right panel shows an absorption spectrum with fluorescence yield detection (integrated between emission energies of 133 and 159 eV), i.e. the S L2,3 emission intensity as a function of excitation energy. With this map, detailed information about the band structure as well as the electronic wave-functions can be obtained.
L. Weinhardt et al., Phys. Rev B79, 165305 (2009).
Under certain conditions electronic states can form quasi-two dimensional states, e.g. inside a thin metallic layer (quantum well state) or at the surface of a metal (e.g. Shockley-type surface states.) In particular the latter can be used as sensitive probes for the modification of surface topology or for the adsorption of atoms and molecules, due to their presence at the surface. On the other hand, these states can play an active role for adsorption or cataclytical properties of a surface. As an example for such a surface state, the figure shows a complete ARUPS data set (He I) of the Shockley state of Cu(111) covered with one atomic layer of Ag-layer. This figure displays the band dispersion vs. the parallel momentum as cuts through the two dimensional k-space.
Forster et al., Phys. Rev. B 84, 075412 (2011).
The broken inversion symmetry at crystal surfaces and interfaces allows for a lifting of the spin-degeneracy and the occurence of spin-polarized states in the electronic structure of two-dimensional systems through the spin-orbit interaction (Rashba-effect). This effect is discussed in the context of electronic applications (e.g. new types of transistors) which make use of the electron spin in addition to the charge, but it is also of high interest for fundamental questions concerning the role of the spin in condensed matter systems. In our group we investigate the Rashba-effect in surface and thin film systems (such as Bi/Cu(111) and Bi/Ag(111)) using ARPES and spin-resolved PES in order to explore its microscopic origin as well as its dependence on geometrical (film thickness, lattice constant, etc.) and chemical (adatoms, adsorbate-substrate combination, etc.) sample parameters.
H. Bentmann et al., Europhys. Lett. 87, 37003 (2009).
H. Bentmann et al., Phys. Rev. Lett. 108, 196801 (2012).
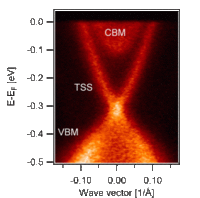
A particular interesting type of two-dimensional electron system are the surface states of topological insulators which, similar to the cases mentioned above, are spin-polarized as a result of the Rashba-effect. These surface states occur within the global energy gap of the bulk insulator and thus open metallic conduction channels in the near-surface region. Unlike conventional surface states, such as e.g. dangling bonds on semiconductor surfaces, topological surface states (TSS) are expected to particularly robust against defects or adatoms as their existence is a consequence of the bulk band topology. We use ARPES, spin-resolved PES, synchrotron-based core level spectroscopy as well as STM to study the influence of adsorbate atoms on TSS and the interface formation between topological insulators, such as Bi2Se3 or Sb2Te3, and metallic overlayers. The figure on the right shows an ARPES spectrum of Bi2Se3(0001) revealing a TSS bridging the energy gap between the conduction band minimum (CBM) and the valence band maximum (VBM) of the bulk.
C. Seibel et al., Phys. Rev. B 86, 161105(R) (2012).
Klassischer Zugang zu topologischer Materie
Die besonderen quantenmechanischen Eigenschaften, die man in topologischen Festkörpern beobachtet, beruhen auf der Wellennatur der Elektronen im langreichweitig geordneten, atomaren Kristallgitter. In verschiedenen verblüffenden Experimenten hat man diese Kristallgitter makroskopisch nachgebildet, um daran Untersuchungen, die auf atomarer Skala oft schwierig oder unmöglich sind, durchzuführen. Diese künstlichen Modellkristalle bestehen aus gekoppelten identischen Oszillatoren, die die Atome des Festkörpers darstellen. Diese "Atome" können mechanische Pendel, elektrische Schwingkreise oder akustische Hohlraumresonatoren für Schallwellen sein, sind also mit vergleichsweise einfachen klassischen Ansätzen beschreibbar. Ihre Größenskala liegt im Bereich einiger Zentimeter.
In Würzburg werden neben den optischen Gittern (TeP) aktuell vor allem zwei weitere Wege verfolgt, nämlich die elektronischen Schwingkreise (EP3) und die akustischen Resonatoren (EP7). Ziel ist es jeweils, die Modellparameter der "Atome" und ihrer gegenseitigen Kopplungen so zu variieren, dass man Anregungszustände erreichen kann, die mit echten Atomen im Gitter noch nicht dargestellt werden können.
Topocoustics
Für die akustischen Resonatoren hat sich der Begriff „Topocoustics“ etabliert, der sich aus den Begriffen „Topologie“ und „Akustik“ zusammensetzt. Bisher wurden am Lehrstuhl EP7 im Rahmen von Abschlussarbeiten im Physikstudium bereits zwei Modellsysteme verfolgt, die sich zunächst durch ihre Dimension unterscheiden: eine eindimensionale Kette mit „zweiatomiger“ Basis sowie ein zweidimensionales hexagonales Gitter.
Die SSH-Kette
Das Su-Schrieffer-Heeger-Modell (SSH) ist ein theoretisches Modell, das zur Beschreibung des (eindimensionalen) Polymers Polyacetylen entwickelt wurde.
Besonders interessant ist das SSH-Modell, da es grundlegende Eigenschaften eines topologischen Isolators aufweist. Das Modell besteht aus einer Kette aus periodisch aneinandergereihten Einheitszellen mit zweiatomiger Basis, in deren Potenzial sich einzelne Elektronen befinden. Die Übergangsrate innerhalb der Basis und zwischen den Einheitszellen wird mit zwei unterschiedlichen Kopplungsparametern beschrieben. Abhängig von der Wahl dieser Kopplungsparameter ergeben sich in diesem Modell charakteristische, so genannte topologisch nicht-triviale Zustände [1,2].

Abbildung 1: Experimenteller Aufbau zur experimentellen Realisierung des Su-Schrieffer-Heeger Modells. Zur Messung werden die Bestandteile (Rohrelemente und Blenden) zusammengeschoben (rechts unten).
In der akustischen Realisierung des SSH-Modells entsprechen die elektronischen Anregungen der atomaren Kette einer Schallwelle. Die einzelnen Atome sind kurze Aluminiumrohre, die durch Blenden mit unterschiedlichem Innendurchmesser miteinander verbunden sind. Die beiden Kopplungsparameter, die jeweiligen Hybridisierungen zwischen Nachbaratomen im SSH-Modell, entsprechen im makroskopischen Modell der Dimensionierung der Löcher in den Blenden (A) und (B) (siehe Abb. 1 und 2).
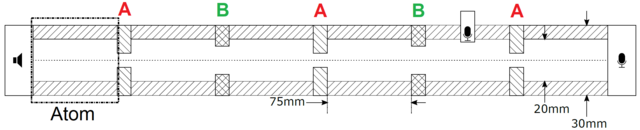
Abbildung 2: Querschnitt des Aufbaus aus Abbildung 1. Ein Lautsprecher, zwei Mikrofone und alternierenden Blenden A und B sind dargestellt. Das zweite Mikrofon wird verwendet, um in jedem einzelnen „Atom“ zu Messen.
In der eindimensionalen akustischen Kette bilden sich dann Zustände aus, bei denen im Gegensatz zum echten Festkörper nicht nur der Betrag der Schwingung, sondern auch direkt die Phase gemessen werden kann. Solche akustischen Schwingungszustände in einer achtatomigen Kette sind in Abbildung 3 dargestellt. Hierbei handelt es sich um die „Wellenfunktionen“ des akustischen Kristalls.
Abbildung 3: Drei gemessene Schwingungszustände im akustischen SSH-Modell. Die Länge der Pfeile repräsentiert jeweils die Lautstärke in einer der hier verwendeten „Atome“ beziehungsweise Kavitäten. Der Winkel zwischen den Pfeilen bezüglich der Drehachse ist die gemessene Phasendifferenz.
Analog lässt sich dem akustischen Festkörper auch eine Bandstruktur zuordnen, bei dem die akustische Frequenz eines Zustandes das Äquivalent zur Energie darstellt.
Das Honigwabengitter
Neben der eindimensionalen SSH-Kette untersuchen wir ein spezielles zweidimensionales akustisches Gitter mit hexagonaler Symmetrie. Das „Honigwabengitter“ hat eine zweiatomige Basis, deren Nachbaratome jeweils drei um 120° zueinander rotierten Atome sind. Die Eigenschaften der elektronischen Zustände (analog: des Schalls) in einem solchen Gitter hängen im Wesentlichen von den Werten für die Nachbarkopplung und den Resonanzfrequenzen der einzelnen Atome ab.
Im einfachsten Fall sind die Resonanzfrequenzen der Basisatome, sowie die jeweiligen Kopplungen identisch, wodurch ein graphenähnliches System modelliert wird. Im Impulsraum bilden sich für die Anregungsenergien bzw. -frequenzen sogenannte „Dirac-Kegel“ aus. Im Bild der Akustik bedeutet das, dass sich Schall unabhängig von der Frequenz in dem Kristall ausbreiten kann, wohingegen sich bei einer anderen Wahl der Parameter Bandlücken im Frequenz- oder Energiespektrum bilden, in denen es keine Anregungen gibt [2,3].

Abbildung 4: Experimenteller Aufbau des hexagonalen akustischen Gitters. Der Abstand der kleinen Resonatorkammern im Zwischenraum zwischen den Streuern, also der Atome, beträgt 3,6 cm. Die Streuer (mit dreieckigem Querschnitt, blau) sind drehbar und erlauben eine kontinuierliche Veränderung der Resonanzfrequenzen der Atome. Die Mikrofon-Öffnungen sitzen an den Positionen zwischen den Streuern und sind während der Messung verschlossen. Anregung erfolgt durch einen Lautsprecher vom Rand aus (rechts).
Der Aufbau ist in Abb. 4 zu sehen. Durch Rotation der blauen Streuer kann zwischen der Topologie eines graphenähnlichen und eines bornitridähnlichen Systems gewechselt werden. Bringt man zwei Gitter, die sich durch die Ausrichtung der Streuer in unterschiedlichen topologischen Phasen befinden, in Kontakt, so bildet sich an der Grenzschicht ein eindimensionaler Kanal aus, der eine Schallwelle innerhalb der akustischen Bandlücke erlaubt [4].
(Fotos: F. Hoffmann und S. Widmann, EP7, Abschlussarbeiten, Univ. Würzburg, 2020)
[1] J. K. Asb´oth, L. Oroszl´any, A. P´alyi: A Short Course on Topological Insulators. arXiv:1509.02295v1
[2] C.L. Kane: Topological Band Theory and the Z2 Invariant
[3] Wang, E., Lu, X., Ding, S. et al.: Gaps induced by inversion symmetry breaking and second-generation Dirac cones in graphene/hexagonal boron nitride. Nature Phys 12, 1111 (2016). https://doi.org/10.1038/nphys3856
[4] Lu, J., Qiu, C., Ye, L. et al.: Observation of topological valley transport of sound in sonic crystals. Nature Phys 13, 369–374 (2017). https://doi.org/10.1038/nphys3999