Physical Review Materials
We present a systematic experimental study of the topological phase transition in a series of ∼10nm thick Hg1−xCdxTe quantum wells by tuning the Cd content x. We provide detailed structural and magneto-optical spectroscopic characterization measurements and establish a comprehensive picture of the alloy structural and energetic properties. Using these as input, we employ k·p modeling to establish the topological phase diagram of Hg1−xCdxTe in dependence on the Cd content and quantum well thickness for thin films which are pseudomorphically strained to the lattice constant of pure CdTe.
SciPost Physics Codebases (Article)
SciPost Physics Codebases (Codebase release)
The software project kdotpy provides a Python application for simulating electronic band structures of semiconductor devices with k·p theory on a lattice. The application implements the widely used Kane model, capable of reliable predictions of transport and optical properties for a large variety of topological and non-topological materials with a zincblende crystal structure. The application automates the tedious steps of simulating band structures. The user inputs the relevant physical parameters on the command line, for example materials and dimensions of the device, magnetic field, and temperature. The program constructs the appropriate matrix Hamiltonian on a discretized lattice of spatial coordinates and diagonalizes it. The physical observables are extracted from the eigenvalues and eigenvectors and saved as output. The program is highly customizable with a large set of configuration options and material parameters.
Physical Review Research
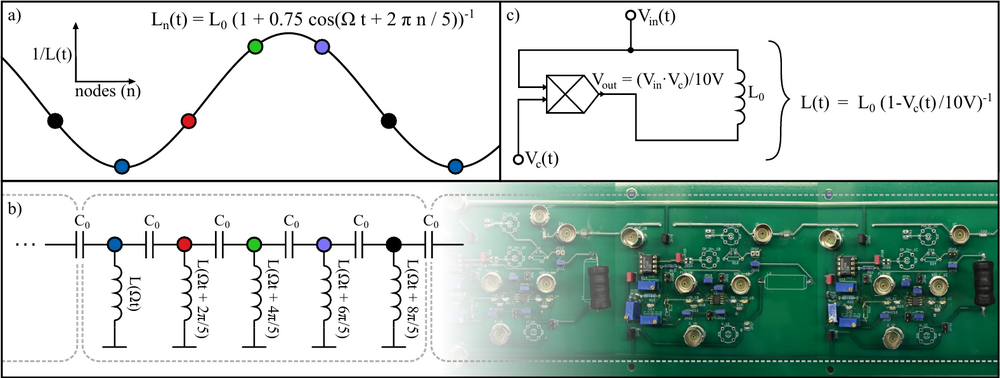
Quantized adiabatic transport can occur when a system is slowly modulated over time. In most realizations, however, the efficiency of such transport is reduced by unwanted dissipation, back-scattering, and nonadiabatic effects. In this paper, we realize a topological adiabatic pump in an electrical circuit network that supports remarkably stable and long-lasting pumping of a voltage signal. We further characterize the topology of our system by deducing the Chern number from the measured edge band structure. To achieve this, the experimental setup makes use of active circuit elements that act as time-variable voltage-controlled inductors.
Physical Review Research
A striking feature of three-dimensional (3D) topological insulators (TIs) is the theoretically expected topological magnetoelectric (TME) effect, which gives rise to additional terms in Maxwell's laws of electromagnetism with an universal quantized coefficient proportional to half-integer multiples of the fine-structure constant α. In an ideal scenario one therefore expects also quantized contributions in the magnetooptical response of TIs. We review this premise by taking into account the trivial dielectric background of the TI bulk and potential host substrates, and the often present contribution of itinerant bulk carriers. We show (i) that one obtains a nonuniversal magnetooptical response whenever there is impedance mismatch between different layers and (ii) that the detectable signals due to the TME rapidly approach vanishingly small values as the impedance mismatch is detuned from zero. We demonstrate that it is methodologically impossible to deduce the existence of a TME exclusively from an optical experiment in the thin film limit of 3D TIs at high magnetic fields.
Journal of Applied Physics
We present a setup for fast, low-bias ( ≤ 1 mV) DC transport measurements with μs time resolution for high ohmic resistance ( ≈ 20 k Ω) semiconducting samples. We discuss the circuitry and instrumentation for the measurement approach that can be applied to any kind of semiconductor device or (gated) two-dimensional material and demonstrate the main measurement artifacts in typical measurements by means of circuit simulation. Based on the latter, we present a simple two-step protocol for eliminating the measurement artifacts reliably. We demonstrate the technique by measuring the transitions between quantum Hall plateaus in the HgTe quantum wells and resolve plateaus as short-lived as 100 μs.
ACS Photonics
Nonlinear phenomena in the THz spectral domain are important for understanding the optoelectronic properties of quantum systems and provide a basis for modern information technologies. Here, we report a giant THz nonlinearity in high-mobility 2D topological insulators based on HgTe quantum wells, which manifests itself in a highly efficient third harmonic generation. We observe a third harmonic THz susceptibility several times higher than that in bare graphene and many orders of magnitude higher than that in trivial quantum well structures based on other materials. To explain the strong nonlinearity of HgTe-based heterostructures at the THz frequencies, we consider the acceleration of free carriers with a high mobility and variable dispersion. This acceleration model, for which the nonparabolicity of the band dispersion is key, in combination with independently measured scattering time and conductivity, is in good agreement with our experimental data in a wide temperature range for THz fields below the saturation. Our approach provides a route to material engineering for THz applications based on frequency conversion.
Physical Review Research
We observe a localized cnoidal (LCn) state in an electric circuit network. Its formation derives from the interplay of nonlinearity and the topology inherent to a Su-Schrieffer-Heeger (SSH) chain of inductors. Varicap diodes act as voltage-dependent capacitors, and create a nonlinear on-site potential. For a sinusoidal voltage excitation around midgap frequency, we show that the voltage response in the nonlinear SSH circuit follows the Korteweg-de Vries equation. The topological SSH boundary state, which relates to a midgap impedance peak in the linearized limit is distorted into the LCn state in the nonlinear regime, where the cnoidal eccentricity decreases from edge to bulk.
Nature Communications
Curved spaces play a fundamental role in many areas of modern physics, from cosmological length scales to subatomic structures related to quantum information and quantum gravity. In tabletop experiments, negatively curved spaces can be simulated with hyperbolic lattices. Here we introduce and experimentally realize hyperbolic matter as a paradigm for topological states through topolectrical circuit networks relying on a complex-phase circuit element. The experiment is based on hyperbolic band theory that we confirm here in an unprecedented numerical survey of finite hyperbolic lattices. We implement hyperbolic graphene as an example of topologically nontrivial hyperbolic matter. Our work sets the stage to realize more complex forms of hyperbolic matter to challenge our established theories of physics in curved space, while the tunable complex-phase element developed here can be a key ingredient for future experimental simulation of various Hamiltonians with topological ground states.